SHARE THE ARTICLE ON
Quadratic regression is the process of finding the equation of a parabola, that best fits your dataset.
You can identify a quadratic regression by the plotting of your scatterplots. If the scatterplots are in a shape looking like a “U” (concave up), or the scatterplot are plotted in a shape like an up-side down U like “∩” (concave down), then you can say that you have a Quadratic regression at your hand which is best fitting your data. The shape of the scatterplots are not always complete. So you might see a half U or just a 3/4th of it.
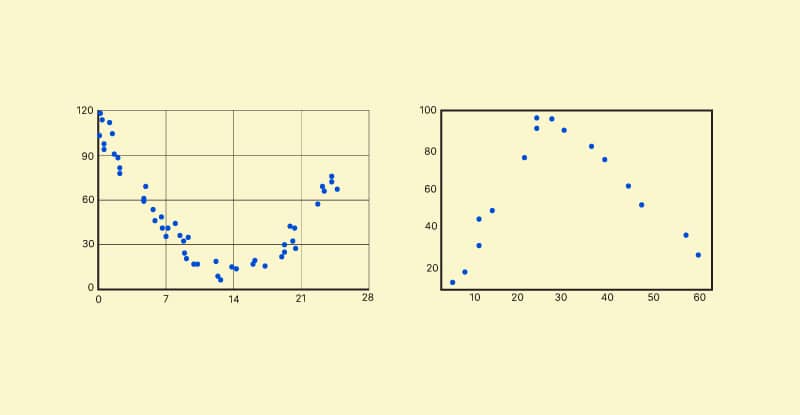
As being an extension of simple linear regression, we can say that the major difference between the both is that in linear regression, a straight line can be drawn using only two points too. But when it comes to Quadratic regression, as it is a parabolic curve, you need as much points as possible to plot a perfect curve. Due to this disadvantage of Quadratic regression, it is generally more costly than simple linear regression.
Create an actionable feedback collection process.
y = ax2 + bx + c
a = { [ Σ x2 y * Σ xx ] – [Σ xy * Σ xx2 ] } / { [ Σ xx * Σ x2 x2] – [Σ xx2 ]2 }
b = { [ Σ xy * Σ x2 x2 ] – [Σ x2y * Σ xx2 ] } / { [ Σ xx * Σ x2x 2] – [Σ xx2 ]2 }
c = [ Σ y / n ] – { b * [ Σ x / n ] } – { a * [ Σ x 2 / n ] }
Where,
a, b, c are the coefficients of Quadratic regression.
Σ x x = [ Σ x 2 ] – [ ( Σ x )2 / n ]
Σ x y = [ Σ x y ] – [ ( Σ x * Σ y ) / n ]
Σ x x2 = [ Σ x 3 ] – [ ( Σ x 2 * Σ x ) / n ]
Σ x2 y = [ Σ x 2 y] – [ ( Σ x 2 * Σ y ) / n ]
Σ x2 x2 = [ Σ x 4 ] – [ ( Σ x 2 )2 / n ]
a, b, c are the coefficients of Quadratic regression.
Let’s take an example to understand how the formula works around the give data.
Example: draw a second degree polynomial with polynomial regression for the given dataset.
x values | y values |
5 | 3 |
6 | 2 |
4 | 4 |
In our case, n=3.
x | y | x2 | x3 | x4 | xy | x2y |
5 | 3 | 25 | 125 | 625 | 15 | 75 |
6 | 2 | 36 | 216 | 1296 | 12 | 72 |
4 | 4 | 16 | 64 | 256 | 16 | 64 |
∑x | ∑y | ∑x2 | ∑x3 | ∑x4 | ∑xy | ∑x2y |
15 | 9 | 77 | 405 | 2177 | 43 | 211 |
Get market research trends guide, Online Surveys guide, Agile Market Research Guide & 5 Market research Template
Σ x x = [ Σ x 2 ] – [ ( Σ x )2 / n ]
∑xx = [77] – [(15)2 / 3]
∑xx = 77 – [225/3]
∑xx = 77 – 75
∑xx = 2
Σ x y = [ Σ x y ] – [ ( Σ x * Σ y ) / n ]
∑xy = [43] – [(15 x 9) /3]
∑xy = 43 – [135/3]
∑xy = 43 – 45
∑xy = -2
Σ x x2 = [ Σ x 3 ] – [ ( Σ x 2 * Σ x ) / n ]
∑xx2 = [405] – [(77 x 15) / 3]
∑xx2 = 405 – [1155 / 3]
∑xx2 = 405 – 385
∑xx2 = 20
Σ x2 y = [ Σ x 2 y] – [ ( Σ x 2 * Σ y ) / n ]
∑x2y = [211] – [(77 x 9) / 3]
∑x2y = 211 – [693 / 3]
∑x2y = 211 – 231
∑x2y = -20
Σ x2 x2 = [ Σ x 4 ] – [ ( Σ x 2 )2 / n ]
∑x2x2 = [2177] – [(77)2 / 3]
∑x2x2 = 2177 – [5929 / 3]
∑x2x2 = 2177 – 1976
∑x2x2 = 201
a = { [ Σ x2 y * Σ xx ] – [Σ xy * Σ xx2 ] } / { [ Σ xx * Σ x2 x2] – [Σ xx2 ]2 }
a = {[-20 * 2] – [-2 * 20]} / {[2 * 201] – [20]2}
a = {(-40) – (40)} / {(402) – (400)}
a = -80 / 2
a = -40
See Voxco survey software in action with a Free demo.
b = { [ Σ xy * Σ x2 x2 ] – [Σ x2y * Σ xx2 ] } / { [ Σ xx * Σ x2x 2] – [Σ xx2 ]2 }
b = {[-2 * 201] – [-20 * 20]} / {[2 * 201] – [20]2}
b = {[-402] – [-400]} / {(402) – (400)}
b = -2 / 2
b = -1
c = [ Σ y / n ] – { b * [ Σ x / n ] } – { a * [ Σ x 2 / n ] }
c = [9 / 3] – {-1 * (15 / 3)} – {-40 * (77 / 3)}
c = 3 – [-1 * 5] – [-40 * 25.66]
c = 3 – (-5) – (-1026.4)
c = 1034.4
y = ax2 + bx + c
y = -40x2 + (-1x) + 1034.4
y = -40x2 – x + 1034.4
Hence, the Quadratic regression equation of your parabola is y = -40x2 – x + 1034.4
Apart from this, there are various online Quadratic regression calculators that make your task easy and save all these steps and give the Quadratic regression equation straight away.
Read more
PATIENT EXPERIENCE PX outlook for 2021: Why patient survey software is going to be vital Free Download: Enhance your Patient Experience program by using these
Product Survey Questions SHARE THE ARTICLE ON Share on facebook Share on twitter Share on linkedin Table of Contents A product survey is a series
Nominal, Ordinal, Interval, Ratio Scales: Examples and Data analysis The ultimate secondary research guide Upgrade your secondary research with agile market research guide. Download Now
Bad Survey Questions: Introduction, Feature, and Questions SHARE THE ARTICLE ON Table of Contents The progress of your survey begins with the sort of questions
Employee engagement survey questions SHARE THE ARTICLE ON Table of Contents WHAT IS AN EMPLOYEE ENGAGEMENT SURVEY? An employee engagement survey is adopted company-wide, involves
The key role of data integration in leveraging the power of machine intelligence Introduction __ Today Artificial Intelligence (AI) is possibly the most widely discussed
Hindol Basu
GM, Voxco Intelligence
English
